پیش‌بینی مسافران نجات‌یافته

در این پروژه سعی خواهم کرد که یکی از مسابقات سایت Kaggle.com که از طریق این [لینک](https://www.kaggle.com/c/titanic) قابل دسترسی می‌باشد را بررسی کنیم. در این مسابقه از شرکت کنندگان خواسته شده که با استفاده از اطلاعات داده شده درباره مسافران کشتی تایتانیک که در مجموعه داده‌[^1]های مسابقه ارایه شده پیشبینی کنند که چه کسی از تایتانیک جان سالم بدر برده است. در ادامه ابتدا توضیحاتی راجع به داده‌های مسئله داده می‌شود سپس تعدادی از روش‌‌هایی که برای حل مسئله مطرح هستند بررسی خواهند شد.
# مقدمه
در حادثه برخورد کشتی تایتانیک به کوه یخ 1502 نفر از 2224 مسافر و خدمه کشتی کشته شدند که یکی از دلایل آن عدم تعبیه قایق نجات به تعداد لازم بود.
هرچند که می‌توان شانس را یکی از عوامل تاثیرگذار در نجات یافتن افراد بیان کرد اما برای برخی افراد مانند زنان و بچه‌ها و افرادی که در قسمت‌های با درجه[^2] بالاتر جای داشتند احتمال بیشتری وجود داشت که نجات پیدا کنند.
داده‌های مسأله بصورت فایل‌های csv [^3] در اختیار کاربران قرار داده شده اند. در شکل زیر اطلاعات داده شده و توضیحات آنها آورده شده است.
![شکل1-اطلاعات داده شده راجع به مسافران](http://i.imgur.com/1MpPa2D.png)
قسمتی از داده‌ها:
![شکل2-قسمتی از داده‌ها](http://i.imgur.com/4wCqrcS.png)
همانطور که در شکل مشخص می‌باشد برای برخی افراد بعضی ویژگی‌ها دارای مقدار نمی‌باشند.
مجموعه داده‌ها دارای 819 نمونه می‌باشد.
مجموعه داده شده جهت تست نیز دارای 418 نمونه است.
در صورتی که یک بررسی اولیه بر روی داده‌ها انجام دهیم نتایج زیر بدست می‌آیند.
![شکل3-بررسی اولیه](http://i.imgur.com/OanANSO.png)
همانطور که مشاهده می‌کنید جنسیت مسافر در نجات یافتن وی بسیار تاثیر گذار می‌باشد چنانکه 74 درصد زنان زنده ماندند در حالی که تنها 18 درصد مردان نجات پیدا کردند. این اطلاعات درک کلی از شرایط مسئله در اختیار ما قرار می‌دهند.
# کارهای مرتبط
در منابع ذکر شده  روش‌های Naïve Bayes، Decision Tree، Random Forest استفاده شده اند که سعی خواهیم کرد هر یک را در حد امکان قابل درک بررسی کنیم. برای هر روش پیشنهادی در ابتدا راجع به کلیت روش توضیح داده شده سپس روش را برای مسئله داده شده بکار خواهیم برد.
## [1]روش Naïve Bayes
در این روش از قوانین احتمال شرطی جهت رسیدن به احتمال زنده ماندن یک فرد استفاده می‌کنیم.
$$P(outcome|evidence)=P(outcome)  \times (evidence | outcome)/P(evidence)$$
(احتمال outcome به شرطی که شرط  evidence محقق شده باشد)
بنابراین زمانی که بخواهیم احتمال زنده ماندن (outcome) را بر اساس یک ویژگی در فرد محاسبه کنیم این رابطه به کمک ما خواهد آمد.
برای مثال می‌خواهیم محاسبه کنیم که اگر شخصی زن باشد
احتمال زنده ماندن آن چه قدر است. اگر p(s)  را احتمال رنده ماندن در نظر بگیریم:
$$P(s|female)=P(s) \times P(female | s)/P(female)$$
که مقادیر (P(s) ، P(female | s و(P(female قابل محاسبه می‌باشند. برای مثال (P(female|s (احتمال زن بودن به شرط زنده ماندن)  نمایان‌گر ان است که چند درصد نجات یافتگان زن می‌باشند که با استفاده از اطلاعات مسئله به سادگی قابل محاسبه می‌باشد.
حال اگر بخواهیم چند شرط را در نظر بگیریم رابطه بالا به شکل زیر در می‌آید:
![Bayes’ theorem ](http://i.imgur.com/HgKEayb.png)
که در این فرمول نیز هرکدام از بخش ها با توجه به اطلاعات مسئله قابل محاسبه می باشند .
در این مرحله احتمال زنده ماندن با در نظر گرفتن ترکیبات مختلفی از ویژگی‌های فرد اندازه گرفته شده است. در صورتی که احتمال بیشتر از 50 درصد بود، فرد را نجات یافته و در غیر این صورت فرد را غرق شده به حساب می‌آورده و نتایج بدست آمده را با اطلاعات مسئله چک می‌کرده تا میزان دقت روش به ازاء ویژگی های در نظر گرفته شده را بدست آید.
![شکل4-نتایج حاصل از روش Naïve Bayes به ازاء ترکیبات مختلف  ویژگی‌های فرد](http://i.imgur.com/JJdEhSu.png)
همانطور که از جدول بالا مشخص می‌باشد فقط با در نظر گرفتن جنسیت افراد دقت 76.79 درصد به دست آمده است. این در حالی است که اضافه کردن ویژگی‌های دیگر نتنها نتایج را بهبود نبخشیده بلکه در مواردی باعث کاهش آن شده است. این موضوع به خاطر تاثیر بسیار زیاد جنسیت می‌باشد. اگر سایر ویژگی‌ها را بدون جنسیت در نظر بگیریم دقت 65.79 درصدی حاصل می‌شود که نمایانگر این موضوع می‌باشد که اگرچه این ویژگی‌‌ها به اندازه جنسیت موثر نمی‌باشند اما همچنان در احتمال زنده ماندن فرد تاثیرگذارند.
##درخت تصمیم[^4][1,2]
درخت تصمیم‌  یکی از روش‌های طبقه بندی[^5] به شکل یک درخت می باشد که:

1. برگ ها مشخص کننده‌ی ویژگی هدف(در اینجا احتمال زنده ماندن) می‌باشند.
2. هر یک از گره‌های میانی نقش یک گره تصمیم‌گیری بر اساس یک ویژگی را ایفا می‌کنند که دارای یک زیر درخت به ازاء هریک از نتایج تصمیم‌گیری می‌باشد
در این درخت سعی می‌شود تا با استفاده از انتخاب شروط مناسب در هر گره تصمیم‌گیری درختی بسازیم که پیشبینی بهتری ارایه دهد.  نمونه‌ای از درخت تصمیم گیری را در شکل زیر مشاهده می‌کنید.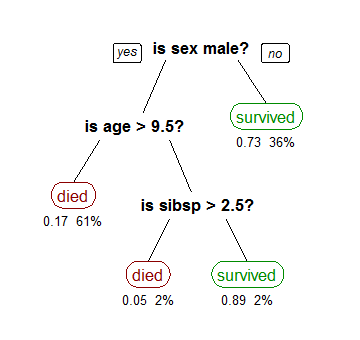
![شکل6-یک نمونه درخت تصمیم](https://upload.wikimedia.org/wikipedia/commons/f/f3/CART_tree_titanic_survivors.png)
در این شکل اگر به یکی از برگ‌های سبز رسیدیم مسافر را نجات‌یافته و در غیر این صورت غرق شده به حساب می آوریم.
الگوریتم‌هایی که برای ایجاد درخت تصمیم استفاده می‌شوند معمولا بشکل بالا به پایین کار می‌کنند به این صورت که در هر مرحله متغیری را که به بهترین شکل مجموعه داده ها را تقسیم می‌کند انتخاب می‌کند. الگوریتم‌های مختلف معیار‌های مختلفی از بهترین ارایه می‌دهند که برای اطلاعات بیشتر می‌توانید به این [لینک](https://en.wikipedia.org/wiki/Decision_tree_learning) مراجعه نمایید.
 نویسنده مقاله مرجع در این روش از ویژگی‌های جنسیت، درجه مسافر، سن و کرایه[^6] استفاده کرده است. در ابتدا داده‌ها صرفا بر اساس جنسیت دسته بندی شده‌اند که دقت 76.79 درصدی حاصل شده است(شکل3). که همانطور که انتظار می‌رفت با نتایج بدست آمده ار روش اول همخوانی دارد چراکه با این شرط هر دو روش به شکلی یکسان با داده برخورد می‌کنند(یعنی مردان را مرده و زنان را نجات یافته به حساب می‌آورند).
در مرحله بعد هرکدام از شاخه‌های مردان و زنان براساس درجه تقسیم بندی شده اند. همانطور که در شکل3 مشخص است برای تمام درجات احتمال زنده ماندن مردان کمتر از 50% می‌باشد که بدین معنی می‌باشد احتمالا بهتر است نتیجه این برگ ها را مرگ در نظر بگیریم. اما شرایط برای زنان بگونه‌ای دیگر است. در شاخه زنان در همه درجات به غیر از درجه 3 احتمال زنده ماندن بیشتر از 50% می‌باشد. اگر نتیجه کلاس 3 را هم زنده ماندن در نظر بگیریم همان نتیجه مرحله قبل(76.79%) بدست می آید چراکه باز هم مردان مرده و زنان نجات یافته به حساب می‌آیند. ولی اگر نتیجه این برگ را مرگ در نظر بگیریم دقت به (77.27%) افزایش می‌یابد.
سپس نوبت به سن می‌رسد. سن یک مقدار نسبتا پیوسته دارد نبابراین تصمیم‌گیری چگونگی انتخاب معیار تصمیم‌گیری بسیار مهم می‌باشد. بصورت کلی افراد با سن کمتر احتمال زنده ماندن بیشتری نسبت به افراد مسن تر داشته اند. در مقاله منبع ذکر شده که بجای اینکه برای همه‌ی درجه های جنسیت ها در درخت، معیار یکسانی انتخاب شود هر کدام از درجه‌ها در هرکدام از جنسیت را بصورت جداگانه مورد بررسی قرار داده تا معیار مناسبی جهت تقسیم بندی هرکدام بر اساس سن انتخاب کنند. انتخاب این معیار براین اساس بوده است که اگر افرادی که سن کمتری از معیار سنی دارند و افرادی که سن بیشتری از معیار سنی دارند را طبقه بندی کنیم خطای طبقه بندی در مجموعه داده آموزشی[^7] کمتر باشد. پس از این کار دقت به 78.94% افزایش یافت.متاسفانه منبع ذکر شده جزئیات بیشتری در رابطه با چگونگی انتخاب معیار‌ها و یا حتی مقدار دقیق معیار‌ها ذکر نکرده است.

##جنگل تصادفی[^8][3,2]
درخت تصمیم‌گیری در عمق‌های زیاد گرایش به یادگیری الگو‌های غیر معمول دارد که باعث بیش‌برازش[^9] بر روی داده‌های آموزشی می‌شود (یعنی بر روی
داده‌های آموزشی بسیار خوب جواب می‌دهد اما بر روی داده‌های جدید دارای خطای زیاد می‌باشد). یکی از روش‌هایی که برای رفع این مشکل پیشنهاد می‌شود استفاده از جنگل تصادفی می‌باشد.
اساس این روش بدین صورت می‌باشد که سعی می‌شود درخت‌های مختلفی را ایجاد کرده و سپس برای بدست آوردن نتیجه نهایی از نتایج این درخت ها میانگین گرفته یا نتیجه‌ای که بیشترین تعداد تکرار را دارد انتخاب می‌شود. برای مثال شکل زیر را در نظر بگیرید 
![شکل7-یک نمونه جنگل تصادفی ساده](http://i.imgur.com/Ebl9HeJ.png)
 حال مسافری زنی که جایگاهی در درجه یک دارد و در (Southampton(s سوار کشتی شده است را در نظر بگیرید. دو درخت اول و سوم فرد را نجات‌یافته طبقه‌بندی می‌کنند در حالی که درخت دوم مرگ مسافر را پیشبینی می‌نماید.بنابراین نجات یافتن به عنوان نتجه بازگردانده می شود در این روش سعی می‌شود که درخت تا حد امکان عمیق شود ولی از آنجایی که روش رشد درخت‌ها مشابه یکدیگر است لازم است که روش‌هایی جهت بوجود آوردن تصادف [^10] استفاده شوند.
اولین روش استفاده از کیسه بندی[^11] می‌باشد که از تکنیک Bootstrap aggregating استفاده می‌کند. در این روش بر روی داده‌های ورودی یک نمونه‌گیری با جایگذاری انجام می‌شود البته به گونه‌ای که واریانس کاهش داده شده تا دقت اگوریتم‌های یادگیری ماشینی افزایش یابد. برای مثال تابع sample در زبان R در مقاله ذکر شده است.
>sample(1:10, replace = TRUE)
>3 1 9 1 7 10 10 2 2 9

همانطور که مشخص می‌باشد نمونه برگردانده شده همچنان دارای 10 عنصر می‌باشد ولی بعضی از عناصر آن تکراری می‌باشند. در این روش بطور میانگین 37% عناصر از ارایه ورودی حذف می‌شوند. بدین صورت درخت‌‌‌هایی که از این ورودی ها ایجاد می‌شوند با هم اندکی متفاوت رشد خواهند کرد ولی همچنان عوامل تاثیر گذاری مانند جنسیت به احتمال زیاد به عنوان اولین معیار تقسیم‌بندی استفاده خواهد شد. برای اینکه این مشکل نیز حل شود از روش دیگری برای ایجاد تصادف  استفاده می‌شود. در این روش بجای استفاده از تمام ویژگی‌های موجود به عنوان معیار تصمیم‌گیری از تعداد محدودی از آنها (معمولا ریشه دوم تعداد ویژگی‌‌ها که در اینجا 10 می‌باشد استفاده می‌شود که عدد 3 را برای این مسئله نتیجه می‌دهد) استفاده می‌شود بدین صورت که در هر گره تصمیم گیری مجموعه متفاوتی از ویژگی‌ها جهت انتخاب ارایه میشوند می‌شوند. برای مثال برای یک درخت،اجازه انتخاب از بین سن، درجه،جنسیت برای اولین معیار تقسیم بندی (root) داده می‌شود در حالی که برای درختی دیگر اجازه انتخاب از بین سن ، تعداد اعضاء خانواده و محل سوار شدن داده می‌شود بنابراین بسیاری از درختان امکان انتخاب جنسیت به عنوان اولین معیار نخواهند داشت. همین روال برای سایر گره های تصمیم گیری طی می شود. بنابراین درخت‌های متفاوت تری تولید خواهند شد. با استفاده از این دو روش مجموعه‌ای از درختان متفاوت خواهیم داشت که برای هر ورودی پس از دادن آن به همه عنوان ورودی همه درخت ها پاسخی که بیشترین تعداد را داشته باشد برخواهیم گزید. در مقاله مربوطه برای پیشبینی سن افرادی که سن آنها ذکر نشده در زبان R با استفاده از کسانی که سن آنها در داده‌ها آورده شده است و با استفاده از تابع rpart  یک درخت تصیمیم با هدف پیشبینی سن ایجاد شده که برای پیشبینی سن افراد فاقد این ویژگی استفاده شده است. پس از جایگذاری سن‌های پیشبینی شده، در زبان R و با استفاده از تابع randomForest ، تعداد 2000 درخت تصادفی ایجاد کرده است. در نهایت نتایجی که از این روش بدست آمده اند دارای دقت 81.342% درصد می‌باشند.
نتایج بدست آمده از روش‌های ذکر شده در شکل زیر مقایسه شده است.
![شکل8-مقایسه نتایج](http://i.imgur.com/KGo6GaP.png)


# آزمایش‌ها
##پیش‌نیاز:
جهت اجرای کد برنامه که از [اینجا](https://github.com/Amir-zsh/Titanic-survivals) قابل دسترسی می‌باشد، نیاز به ماژول‌هایی می‌باشد که در فایل requirements.txt موجود در لینک داده شده ذکر شده اند.
برای نصب ماژول‌ها دو راه وجود دارد:
راه اول: همان ابتدا با استفاده از دستور زیر ماژول‌های موجود در فایل را نصب کنید. این روش معمولا به خطا می‌انجامد چراکه بعضی از ماژول‌ها به راحتی قابل نصب نمی‌باشند.
>pip install –r requirements.txt

روش دوم: نرم‌افزار miniconda متناسب با سیستم عامل خود را از [اینجا](http://conda.pydata.org/miniconda.html) دریافت و نصب نمایید. Conda یک برنامه package manager می‌باشد که روش سریعی را جهت استفاده از package ها فراهم می‌آورد. پس از اینکه مراحل نصب تمام شد با استفاده از دستور  conda create -n myenv python  یک virtual environment بسازید و با دستور activate myenv آنرا فعال کنید(می‌توانید از اسم دلخواه خود به جای myenv استفاده نمایید). اکنون با دستور conda install numpy ماژول numpy را نصب کنید. سایر ماژول ها با استفاده از دستوری که در روش اول ذکر شد قابل نصب می‌باشند. 
##پیش‌پردازش:
داده‌های مسئله را می‌توانید که سایت مسابقه در یافت شده اند داخل پوشه data در صفحه github پروژه قابل دسترسی می‌باشد. برای اینکه داد‌‌ه‌ها در الگوریتم‌های بکار رفته قابل استفاده باشد، لازم است که یک عملیات پیش‌پردازش بر روی آنها انجام شود. برای خواندن و پردازش فایل‌های CSV از کتابخانه pandas پایتون استفاده شده است.
همانطور که گفته شد داده‌های مسئله دارای دو فایل train.csv و test.csv می‌باشد ولی از آنجایی که داده‌های موجود در فایل test.csv حاوی
ستون نشان دهنده‌ی نجات یافتن یا نیافتن نمی‌باشند برای بدست آوردن دقت نتایج حدس زده شده لازم است که آنها در صفحه مسابقه قرار دهیم که این کار زمانبر می‌باشد. جهت سادگی کار داده‌های train.csv را که حاوی اطلاعات کامل می‌باشند را به دو قسمت بصورت 30% برای تست و 70% برای یادگیری تقسیم می‌کنیم تا فرایند آزمایش بصورت آفلاین قابل انجام ‌باشد.
بسیاری از داده‌های داده شده دارای مقادیر غیر عددی می‌باشند که لازم است جهت کارکرد صحیح روش‌ها به مقادیر عددی تبدیل شوند. همچنین مقادیر بسیاری از سطر‌های جدول دارای مقادیر null می‌باشند که این مقادیر قابل قبول نمی‌باشند. این سطر‌ها را می‌توان حذف کرد یا مقداری را در خانه‌های خالی جایگزین نمود. در پیاده‌سازی این قسمت با استفاده از تابع interpolate(درون‌یابی) موجود در کتابخانه pandas مقادیر خالی سن جایگزین شده‌اند.ستون cabin را به علت تعداد زیاد مقادیر null، ستون name و ستون ticket را نیز به این دلیل که برای هر فرد منحصر به فرد می‌باشد و یافتن روابط در آنها دشوار می‌باشد از داده‌ها حذف می‌کنیم. ستون‌های دارای مقادیر غیر عددی یا ستون‌هایی که عدد آنها نشان دهنده مقدار آنها نمی باشد را نیز به ستون‌هایی، به تعداد مقادیر مختلفی که می‌توانند داشته باشند تقسیم می‌کنیم ‌برای مثال ستونPclass که می‌تواند دارای مقادیر 1،2یا3 باشد، به سه ستون 1و2و3 تقسیم می‌شود که برای فردی که در کلاس 3 بوده این ستون‌ها به ترتیب مقادیر 0و0و1 خواهند داشت. اکنون سطر‌هایی را که که هنوز دارای مقادیر null می‌باشند حذف می‌کنیم با انجام این کارها از 891 سطر موجود 889 سطر را جهت استفاده خواهیم ‌داشت. مراحل ذکر شده در فایل DataManipulate.py قابل مشاهده می‌باشند. همچنین این فایل حاوی تابعی برای محیا کردن داده‌های فایل تست می‌باشد که در این فاز مورد استفاده قرار نگرفته است.
##روش‌ها:
###درخت تصمیم:
درخت تصمیم در قسمت کار‌های مرتبط توضیح داده شد. نتایج در هر بار اجرا متفاوت می‌باشد لذا میانگین 20 بار اجرا در نظر گرفته شده است  نتایج بدست آمده در جدول زیر آورده شده.
![شکل9-نتایج آرمایش  درخت تصمیم](http://i.imgur.com/UhxVsqc.png)
همانطور که انتظار می‌رفت درخت در عمق‌های زیاد دچار بیش‌برازش[^9] می‌شود.
پیاده سازی این قسمت در فایل DecitionTree.py آورده شده است.
###جنگل تصادفی:
این روش نیز در کارهای مرتبط توضیح داده شده است. مانند روش قبل میانگین 20 بار اجرا در نظر گرفته شده است و نتایج در جدول زیر آورده شده است.
![شکل10-نتایج آرمایش روش جنگل تصادفی](http://i.imgur.com/PbJw1wV.png)
پیاده سازی این قسمت در فایل RandomForest.py آورده شده است.
###افزایش شیب‌دار[^12]:
در این روش ایده اصلی این می‌‌باشد که یک سری از درختان ایجاد کنیم که هر درخت سعی در تصحیح پیشبینی‌‌هایی دارد که درخت پیشین اشتباه انجام داده است. سرانجام پاسخ نهایی می‌تواند برای مثال ترکیبی وزن‌‌دار از پاسخ هر یک از درخت ها می‌‌باشد. با استفاده از این روش و بدون میانگین‌گیری نتایج ثابت زیر بدست می‌‌آیند:
آزمایش روی مقادیر train شده : 0.90850.
آزمایش روی مقادیر train نشده: 0.8134.
پیاده سازی این قسمت در فایل GradientBoost.py آورده شده است.
###شبکه‌های عصبی[^13]:
شبکه‌های عصبی مدلی می‌باشند که با الهام از سیستم‌های زیستی بوجود آمده‌اند. در یک شبکه از عصب‌های زیستی مانند مغز عصب‌ها سلول‌های جداگانه‌ای می‌باشند که ورودی دریافت کرده بر روی آن عملیات انجام می‌دهند سپس حاصل را به عصب یا عصب‌های دیگری که به آنها متصل می‌باشند منتقل می‌نمایند. این را رفتار را ‌می‌توان با استفاده از یک عصب مصنوعی مدل سازی نمود.
![شکل11-یک عصب در شبکه عصبی](http://i.imgur.com/bQjkEFQ.png)
  شکل بالا یک عصب را نشان می‌دهد که ورودی‌هایی را دریافت کرده با استفاده از  f آنها را پردازش می‌کند و خروجی‌هایی را تولید می‌نماید. می‌توان مجموعه‌ای از این عصب‌ها را در چند لایه بصورتی که در شکل زیر مشاهده می‌کنید بکار برد.
  ![شکل12-یک شبکه عصبی با چهار لایه](http://i.imgur.com/JUZGeEe.png)
   یک لایه مربوط ورودی(input) می‌باشد. تعداد عصب‌ها در این لایه معمولا با تعداد ویژگی‌ها ( در اینجا سن، کلاس، جنسیت، ...) برابر می‌باشد.  یک شبکه عصبی می‌تواند فاقد لایه میانی(hidden) باشد یا شامل یک یا چند لایه از این نوع باشد. (در آزمایش یک لایه میانی در نظر گرفته شده است).لایه آخر که لایه خروجی (output) نام دارد نیز می‌تواند شامل یک یا چند عصب بسته به طراحی شبکه باشد (در این آزمایش یک عصب برای این لایه در نظر گرفته شده است).  همچنین در این شبکه هر ارتباط بین عصب‌ها دارای یک وزن می‌باشد. بنابراین برای مثال در شکل بالا تابع فعال سازی برای عصب Hidden 1 به شکل زیر می‌باشد.
   
$$h_1 = f(w_{1,1}\cdot i_1, w_{2, 1}\cdot i_2, w_{3,1}\cdot i_3, w_{4,1}\cdot i_4)$$
 یکی از تابع‌های فعال سازی معمول تابع logistic می‌باشد. که یکی از مزایای آن این است که قابل مشتق‌گیری ‌می‌باشد. در زیز فرمول تابع را مشاهده می کنید.
 $$f(x_1, x_2, \ldots) = \frac{1}{1 + e^{-x_1-x_2-\ldots}}$$
 روش یادگیری:  داده ها در یک شبکه عصبی در دو حالت جریان پیدا می‌کنند. حالت اول زمانی که شبکه در حال یادگیری می‌باشد. حالت دوم زمانی است که شبکه درحالت عادی (پس از یادگیری ‌می‌باشد). داده‌ها از طریق عصب‌های ورودی وارد می‌شوند و پس از عبور از لایه‌های میانی وارد عصب‌های خروجی ‌می‌گردند.  این روش طراحی feedforward نامیده می‌شود. شبکه‌های عصبی با استفاده از یک عنصر بازخورد یادگیری که backpropagation نامیده می‌شود یادگیری می‌کنند. در این روش مقادیری که در شبکه تولید می‌شود با مقادیری که ‌می‌بایست تولید شود مقایسه می‌گردد و از تفاوت بین انها برای اصلاح وزرن‌های بین ارتباطات استفاده می‌شود. این فراید از لایه خروجی، سپس به لایه‌های میانی و سرانجام، به لایه ورودی به طرف عقب می‌رود.
در پیاده سازی این قسمت از ماژول neurolab در زبان پایتون و شبکه feed forward multilayer perceptron استفاده شده است. در ماژول ذکر شده الگوریتم‌های زیادی برای برای یادگیری درنظر گرفته شده است. در پیاده از بین الگوریتم‌های ارایه شده برای MLP[^14]  از الگوریتم Rprop[^15] استفاده شده است. سایر الگوریتم‌ها یا نتیجه‌ی مطلوبی نداشتند یا اینکه به دلیل نامعلومی به سرعت فرایند یادگیری را پایان می‌دادند. برای خروجی یک عصب در نظر گرفته شده است. اگر مقدار عصب بیشتر از ۰.۵  بوده باشد فرد زنده و در غیر اینصورت غرق شده پیشبینی شده است.  قبل از بررسی نتایج لازم است که عبارت epoch توضیح داده شود. Epoch یک تکرار کامل روند یادگیری داده‌های داده شده جهت یادگیری می‌باشد. 
نتایج در جدول زیر آورده شده است.
سعی شده مقادیر به گونه در نظر گرفته شوند که نشان دهنده تاثیر تعداد Epoch‌ها و تداد عصب‌های میانی باشند.نتایج در جدول زیر آورده شده است.
 ![شکل13-نتایج آزمایش شبکه عصبی](http://i.imgur.com/5MuDX4l.png)
 پیاده سازی این قسمت در فایل NeuralNetwork.py آورده شده است.
 از جمله کارهایی می‌توان در فاز بعد جهت بهینه کردن نتایج انجام داد استفاده از روش‌هایی جهت حدس دقیق‌تر مقادیر null و استفاده از داده‌های test جهت گرفتن نتیجه روش‌های بکار رقته از سایت مسابقه می‌باشد.
# کارهای آینده

# مراجع
[1]Eric Lam,Chongxuan Tang.(2015).Titanic – Machine Learning From Disaster
[2]Xiaodong Yang .(2015).Titanic – Machine Learning From Disaster
[3]Kunal Vyas, Zeshi Zheng, Lin Li.(2015).Titanic - Machine Learning From Disaster

**پیوندهای مفید**
+ [صفحه این مسابقه](https://www.kaggle.com/c/titanic)
+ [درخت تصمیم](https://en.wikipedia.org/wiki/Decision_tree_learning)
+ [توصیح تصویری درخت تصمیم](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/)
+ [روشnaive bayes](http://scikit-learn.org/stable/modules/naive_bayes.html)
+ [توضیحnaive-bayes به زبان ساده ](https://stackoverflow.com/questions/10059594/a-simple-explanation-of-naive-bayes-classification/20556654#20556654)
+ [آشنایی با یادگیری ماشینی](http://www.toptal.com/machine-learning/machine-learning-theory-an-introductory-primer)
+ [توضیح درخت تصمیم](http://dms.irb.hr/tutorial/tut_dtrees.php)
+ [جنگل تصادفی](https://en.wikipedia.org/wiki/Random_forest)


[^1]:dataset
[^2]:class
[^3]:Comma-separated values
[^4]:decision tree
[^5]:classify
[^6]:fare
[^7]:training data
[^8]:ramdom forest
[^9]:overfit
[^10]:randomness
[^11]:bagging
[^12]:Gradient Boosting
[^13]:Neural Networks
[^14]:multi layer perceptron
[^15]:resilient backpropagation