یکی از نیازهای صنایع سنگ کشورمان دستگاه تشخیص و جداسازی سنگ های تزیینی است. این دستگاه باید قادر باشد با دریافت نوع های مختلف سنگ، الگوی بافتی آن ها را یادبگیرد و برای نمونه های شناخته نشده، دسته مناسب را تعیین کند
در این پروژه داده های خام، تصاویر سطح سنگ هستند باید با استفاده از مکانیزمی، ویژگی های بافت تصاویر را برای استفاده در دسته بندی استخراج کنیم یک تصویر چیزی نیست جز یک ماتریس که هر درایه آن توصیفگر یک سلول رزولوشن تصویر است.
مکانیزم مورد استفاده باید قادر باشد وابستگی های بین این سلول ها را به خوبی تصویر بکشد و انتزاعی مناسب از این ویژگی ها به دست دهد.

۱. مقدمه

تشخیص نوع و دسته بندی تصاویر، از پرکاربردی ترین مسائل در زمینه ی بینایی ماشین بوده که شامل دو مرحله اصلی استخراج خصوصیات تصویر و تشکیل مدل دسته بندی می باشد بافت تصویر از جمله ویژگی هایی است که در پردازش تصاویر و تشخیص الگو استفاده می شود.دسته بندی در حوزه ی یادگیری ماشین، با داده های برچسب دار در ارتباط است. این بدان معنی است که این داده ها در دسته بندی های متمایز قرار می گیرند و نمونه ی مجهول براساس ویژگی هایش در یک دسته بندی قرار میگیرد. بنابراین لازم است که براساس ویژگی های داده های آموزش مدلی بیابیم که خصوصیات یک نمونه مجهول را به عنوان ورودی دریافت نماید و برچسب آن را به عنوان خروجی ارائه دهد.
دسته بندی بافت سنگ ها یکی از مهمترین چالش های مسائل دسته بندی است. زیرا سنگ های طبیعی دارای بافت هایی کاملا مختلف هستند.از آنجا که سنگ های طبیعی به طور گسترده ای برای دکوراسیون استفاده می شوند، دسته بندی سنگ ها در زمینه های صنعتی بسیار مورد نیاز است .

۱.۱. شرح مساله

همانطور که پیشتر اشاره شد، کاربرد وسیع سنگ های طبیعی در صنعت و ضرورت دسته بندی سنگ ها بر اساس ویژگی های بافتی آنها موجب شده است تلاش هایی برای یافتن راه کار هایی جهت خودکار نمودن فرایند دسته بندی بدون حضور انسان صورت گیرد.

۱.۱.۱. هدف

هدف این پروژه، تعیین معدن سنگ برای نمونه های جدید با استفاده از ویژگی های بافتی آن ها است. در این پروژه نمونه هایی از 4 نوع سنگ متعلق به معادن مختلف مورد بررسی قرار می‌گیرند. همچنین سعی بر آن است که در راستای این هدف ویژگی های بافت تصاویر برای دسته بندی سنگ ها استخراج شود.

۱.۱.۲. داده ها

داده های خام، تصاویر سطح سنگ ها می باشد که در قسمت پیوند های مفید به عنوان مجموعه داده آموزشی قرار داده شده است.

۱.۱.۳. اصطلاحات

• بافت :بافت را می توان به صورت یک تابع از تغییرات مکانی شدت روشنایی پیکسل ها تعریف نمود، بافت اندازه گیری میزان تغییرات هر سطح است که خصوصیاتی مانند همواری و نرمی زبری و منظم بودن هر سطح جهت وتفاوت های منظم را اندازه گیری می کند. تشخیص بافت در سیستم بینایی بشر به راحتی قابل تشخیص است اما در بینایی ماشین و پردازش تصویر پیچیدگی­ های خاص خود را دارد. استخراج بافت در پردازش تصویر و بینای ماشین دارای کاربردهای فراوانی است. از این کاربردها به مواردی نظیر تشخیص اشیا در تصاویر پزشکی و یا ردیابی اشیا در ویدئو­ها، تشخیص کیفیت در صنعت برای افزایش مرغوبیت کالاها، کنترل از راه دور نواحی زمین و تقسیم بندی نواحی زمین از نظر مواردی مانند آب ، اراضی کشاورزی و... می­ توان اشاره کرد.

• سطوح تیرگی¹ :مقداری است که به نمایندگی از میزان روشنایی یک پیکسل از سیاه تا سفید تعیین می گردد.این مقدار معمولا بین صفر (سفید) تا 255(سیاه) می باشد.

۱.۱.۴. محدودیت ها

یکی از محدودیت های موجود در این گونه مسایل این است که پردازش تصویر تنها با تصاویری از سطوح در ارتباط است، این در حالی است که سطوح یکسان ممکن است بافت هایشان هنگامی که تصاویری که در شرایط متفاوت از آنها گرفته می شود، با یکدیگر متفاوت باشند.با داشتن اطلاعات بیشتر از سطوح و تعداد تصاویر بیشتر ممکن است بتوان این محدودیت ها را رفع نمود[2].

۲. کارهای مرتبط

۲.۱. بافت های قابل تفکیک

ژولز ²مفهوم بافت را در زمینه ی تفکیک بافت ها مورد بررسی قرار داده است. او بر روی آماره های فضایی سطوح تیرگی تصویر تمرکز کرد. در ادامه به معرفی آماره های دسته اول³ و آماره های دسته دوم⁴ در تحلیل بافت پرداخته شده است.
آماره های دسته اول : این آماره ها شباهت مقدار تیرگی مشاهده شده در یک ناحیه تصادفی از تصویر را اندازه گیری می کنند. این آماره ها می توانند از هیستوگرامی از درجه ی تیرگی نقاط در تصویر محاسبه گردند. آماره های دسته اول به مقادیر تیرگی پیکسل ها بستگی دارد. اما به تعامل و همبستگی مقادیر پیکسل های مجاور وابسته نمی باشد. برای مثال ، میانگین درجه ی تیرگی در یک تصویر یک آماره ی دسته اول می باشد.
آماره های دسته ی دوم: این آماره ها میزان شباهت یک جفت پیکسل را اندازه گیری می کند که در نقاط انتهایی یک محور با طول تصادفی که بر مکانی خاص و با جهت یابی خاص بر روی تصویر قرار می گیرند[1].
ژولز دو بافتی را که آماره های دسته دوم یکسان هستند را غیر قابل تمایز توسط انسان دانست[12].اما نادرستی این حدس بعد ها توسط خود ژولز اثبات گردید[13] .این امر موجب شد که ژولز نظریه بافت واره ها ⁵ را مطرح کند تا غیرقابل تمیز بودن جفت بافت ها را شرح دهد.بافت واره ها رویداد های بصری (نظیر خاتمه ⁶ و بسته شدن ⁷)هستند که در فرایند تفکیک بافت حضور دارند.خاتمه ها در واقع نقاط انتهایی خطوط یا گوشه ها می باشند.ژولز ملاحظه کرد که تمیز دادن بافت توسط انسان را می توان با تراکم مرتبه اول از بافت واره ها مدل کرد[14].

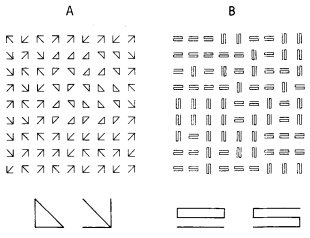
در (تصویر 1)، بر اساس نظریه بافت واره ها ، ناحیه ی سمت راست بالای بافت a از بافت پس زمینه قابل تفکیک است زیرا عناصر در تعداد خطوط انتهایی متفاوت هستند .اما همان ناحیه در بافت b قابل تمایز نیست زیرا هر دو المان دارای تعداد خطوط انتهایی یکسانی هستند[11].
به تشخیص نواحی تصویر با استفاده از ویژگی های بافت ،دسته بندی بافت گفته می شود.هدف از دسته بندی بافت به دست آوردن یک نقشه می باشد که تصاویر مختلفی را به عنوان ورودی دریافت می کند و دسته ی آنها را تعیین می نماید.
اگر قادر به تعیین دسته ی بافت های موجود در تصویر نباشیم اما بتوانیم مرز بافت ها را مشخص کنیم با دسته ی دیگری از مسائل به نام قطعه بندی بافت ⁸ مواجه می شویم.هدف از قطعه بندی تصویر به دست آوردن نقشه ای است که از طریق آن مرزبافت ها به خوبی مشخص گردد[2].

۲.۲. روش های تحلیل بافت

اولین مرحله در راستای ایجاد یک مدل ریاضی برای بافت، تشخیص جنبه های درک شده در یک تصویر است. معمولا بافت توسط تغییرات دو بعدی در تصویر مشخص می شود.
بافت تصویر دارای تعدادی ادراکات است که نقش مهمی را در توصیف بافت ایفا می کنند. بعضی از ویژگی هایی که در توصیف بافت بسیار مؤثر می باشند،عبارتنداز:
یکنواختی، تراکم، زبری، سفتی، نظم، خطی بودن، جهت دار بودن، فرکانس و فاز. بنابراین به دلیل ابعاد گسترده مفهوم بافت، تنها یک روش برای ارائه و مشخص کردن بافت کافی نیست.
اکثر تحلیل های بافت را می توان به چهاردسته ی روش های آماری، روشهای ساختاری یا هندسی، روشهای تبدیلی و روش­های مبتنی بر مدل، تقسیم کرد که در ادامه به شرح آن ها پرداخته شده است.

۲.۲.۱. روش های آماری

اطلاعات مربوط به بافت از خصوصیات آماری پیکسل ها استخراج می شود ، که از جمله اولین روش­های استخراج بافت هستند. یکی از ویژگی های کیفی بافت، توزیع فضایی مقدار تیرگی است. وابستگی فضایی سطوح تیرگی، ویژگی های وابسته به آماره های دسته ی دوم تصویر را تخمین می زند.در همین راستا ما از مجموعه زیر برای معادل سازی یک تصویر N\times N با سطح تیرگی G استفاده می کنیم:

.۲.۲.۱.۱.ماتریس تکرار⁹

درایه ی ( i,j ) از ماتریس تکرار سطوح تیرگی G\times G با نام { p }_{ d } برای بردار d=({ { d }_{ x },d }_{ y }) ، برابر با تعداد تکرار جفت مقادیر i و j با فاصله d در سطوح تیرگی تصویر است.
در (تصویر 2) نمونه ای از ایجاد ماتریس تکرار سطوح تیرگی را مشاهده می کنید:

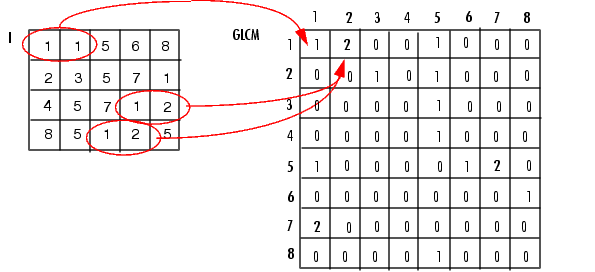
ماتریس تکرار متقارن نیست ، اما اگر ماتریس p را به گونه ای تعریف کنیم که { p }_{ d }+{ p }_{ -d } برقرار باشد ، می توان به یک ماتریس متقارن دست یافت.
هارالیک برای اولین باراستفاده از ماتریس تکرار را پیشنهاد داد که امروزه از پر استفاده ترین روش های استخراج ویژگی های بافتی محسوب می شود. او تعدادی ویژگی بافتی مفید نظیر زاویه، کنتراست، میانگین واریانس و … معرفی کرد که این ویژگی ها از ماتریس تکرار قابل محاسبه می باشند.اما آنها در فواصل مختلف در جهت های مختلف هستند.این فرایند پیچیدگی محاسباتی و زمانی را افزایش می دهد. حتی اگر تمام ویژگی های مورد استفاده قرار گیرند ، نرخ طبقه بندی صحیح می تواند به 60-70٪ برسد[15]که این مقدار توانست با تمرکز تنها بر روی سطوح تیرگی تصاویر به 80% برسد[16] .ویژگی های بافتی که به وسیله ی ماتریس تکرار به دست می آیند، در مسائل جداسازی بافت های تصویر کاربردی نداشته و بیشتر در زمینه ی دسته بندی استفاده می شود[1].

.۲.۲.۱.۲.روش بردار اختلاف سطوح تیرگی(Gray-Level Difference Vector;GLDV ) :

این روش تابع چگالی احتمال را برای اختلافات مقادیر تابع در موقعیت های با فضای d پیکسل دورتر و با زاویه ی s تخمین می زند. اندازه گیری های بافت حاصل بر اساس آماره های دسته ی اول می باشد. در حالی که اندازه گیری های حاصل در روش ماتریس تکرار بر اساس آماره های دسته ی دوم می باشد [4].

۲.۲.۱.۳.ویژگی های مربوط به همبستگی [^Auto-correlation Features]:

تابع همبستگی یک تصویر برای دستیابی به میزان نظم و نیز نرمی و سختی بافت های موجود در تصویر به کار برده می شود. تابع همبستگی تصویر (I(x,y به شکل زیر تعریف می شود:

همچنین تابع همبستگی به طیف توان سری فوریه وابسته است. روش های جدید که از این ویژگی های طیفی استفاده می کنند، دامنه فرکانس را در حوزه ی فرکانس، به حلقه ها و در حوزه ی جهت، به محورها تقسیم می کند. بنا براین در حوزه ی فرکانس، انرژی کل به حلقه ها تقسیم می شود و هرکدام از نواحی به عنوان ویژگی های بافتی محاسبه می شوند.

۲.۲.۲. روش های هندسی

بافت بر اساس ترکیبی از ساختارهای اولیه بافت شامل اپراتور مورفولوژیک و گراف همجواری، که براساس قوانینی تعریف شده اند شناخته می شود مانند استفاده از فیلترهای آشکارساز خط با اپراتورهای مورفولوژیکی، این روش برای بافت های با ساختار منظم و ویژه مانند ساختارهای با خطوط موازی افقی یا عمودی مناسب است ولی برای بافت های نامنظم روش بهینه ای نیست و بیشتر برای ترکیب بافت استفاده می ­شوند تا تحلیل آن. روش های هندسی با وجود اینکه تعریف دقیقی از بافت ارائه می­ دهند، از بازده مناسبی برخوردار نیستند.

۲.۲.۲.۱.روش موزاییک بندی ورونوی ( voronoi )

یکی ازروش های موجود این است که تصاویر به تصاویر موزائیکی تبدیل می شود. در این روش، اشکال از مناطق کوچک درتصویر موزاییک با استفاده از نمودار ورونی تقریب زده می شود. در این نمودار به هر مجموعه‌ای از نقاط ناحیه‌ای اختصاص داده می‌شود. این نواحی سلول‌های ورونوی نامیده می‌شود. برای یک مجموعه از نقاط نمودار ورونوی سطح را به مناطقی تقسیم بندی می‌کند که برای هر نقطه از مجموعه نقاط یک منطقه تعریف می‌شود. به طوری که تمام نقاط این منطقه به نقطه تولید کننده آن منطقه نزدیکتر می‌باشد[5].تصویر موزاییک به طور خودکار با ایجاد تولید نمودار بهینه ورونی به طوری که خطای بینتصویر اصلی و تصویر حاصل تا جایی که ممکن است کوچک می شود.ویژگی های هندسی چند ضلعی های ورونوی به عنوان ویژگی های بافن مورد استفاده قرار می گیرند[6].

۲.۲.۳. روش های تبدیلی و پردازشی

در این روش ها تصویر به فرم جدید تبدیل می شود به طوری که بافت در این فضای جدید راحت تر قابل تشخیص باشد. این روش­ ها سعی می­کنند تا ویژگی­ های معینی از تصاویر فیلتر شده را برای کاربردهای طبقه ­بندی یا تقسیم بندی محاسبه کنند. انواع زیادی از روش­های استخراج ویژگی بر پایه پردازش سیگنال از قبیل ویژگی های تامورا، تبدیل موجک و غیره است که مبتنی بر اعمال فیلتر بر روی تصویر می ­باشند.

۲.۲.۴. روش های مبتنی بر مدل

روش­های مبتنی بر مدل، به مدل سازی بافت می ­پردازند و شامل روش خود بازگشت یا AR مدل گوسی مارکوف یا RMF و مدل Gibbs RMF می ­شوند. در این روش مدلی از تصویر ایجاد می شود و سپس از این مدل برای توصیف سنتز تصویر استفاده می شود. پارامترهای مدل ویژگی های کیفی اساسی بافت را استخراج می کنند[3].

مدل خود بازگشت[^Autoregressive (AR) model]:

مدل خودبازگشت فرض می کند که یک تعامل محلی بین پیکسل های تصویر در آن شدت پیکسل ، مجموع وزن دار شدت پیکسل های همسایه می باشد[7].

مدل فیلد های تصادفی [^Markov random fields]:

این مدل یک فرایند احتمالاتی است که در آن همه تعاملات محلی می باشد. احتمال این که یک سلول در حالت داده شده می باشد، به طور کامل توسط احتمال های حالت سلول های همسایه تعیین می شود. تعامل مستقیم تنها بین همسایگان بلافاصل رخ می دهد[7].

۲.۳. روش های دسته بندی

دسته بندی به عملیات یادگیری تابع f گفته می شود که هر مجموعه ویژگی x را به یکی از دسته های از پیش تعریف شده ی y نگاشت می دهد. به این تابع مدل دسته بندی نیز می گویند که شامل مدل های توصیفی و مدل های پیشگویانه می باشد. مدل توصیفی، مدلی است که به عنوان ابزار توضیحی برای تشخیص اشیا از دسته های مختلف به کار می رود و مدل پیشگویانه به مدلی گفته می شود که می تواند برچسب دسته یک رکورد شناخته نشده را تخمین زند.روش های دسته بندی برای ساخت مدل های دسته بندی از مجموعه های داده ای به می روند.این روش ها دارای یک الگوریتم یادگیری برای توصیف مدل می باشند.مدلی ساخته شده به وسیله ی این الگوریتم ها باید داده های ورودی را به خوبی تطبیق دهد و بتواند برچسب رکورد هایی را که تا کنون ندیده است، تخمین زند. به این منظور ابتدا یک مجموعه آموزش که شامل داده های با برچسب معین است فراهم می شود ،سپس از این مجموعه یک مدل دسته بندی تهییه می گردد.این مدل به مجموعه ی آزمون که شامل داده های با برچسب نا مشخص است، اعمال می شود. کارایی این مدل دسته بندی با بررسی تعداد تخمین های درست و غلطی که توسط مدل صورت گرفته ارزیابی می شود. در ادامه به معرفی دو روش مهم دسته بندی اشاره شده است :

۲.۳.۱. درخت تصمیم

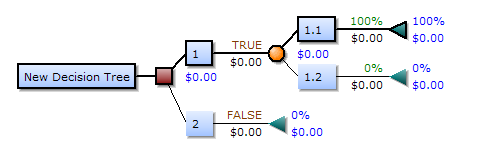
درخت تصمیم یک ابزار برای پشتیبانی از تصمیم است که از درختان برای مدل کردن استفاده می‌کند. در آنالیز تصمیم، یک درخت تصمیم به عنوان ابزاری برای به تصویر کشیدن و آنالیز تصمیم، در جایی که مقادیر مورد انتظار از رقابت‌ها متناوباً محاسبه می‌شود، استفاده می‌گردد. یک درخت تصمیم دارای سه نوع گره‌ است:

• گره تصمیم: به طور معمول با مربع نشان داده می‌شود.

• گره تصادفی: با دایره مشخص می‌شود.

• گره پایانی: با مثلث مشخص می‌شود.

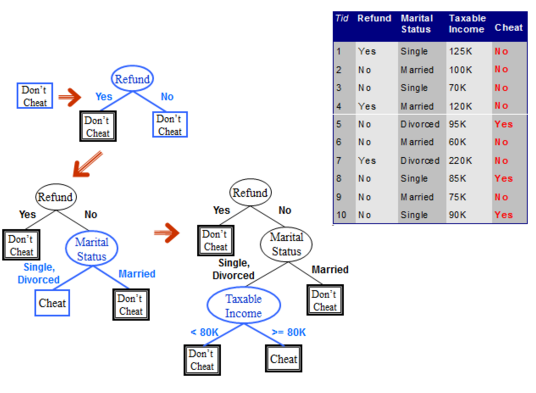
مربع نشان دهنده تصمیم، بیضی نشان دهنده فعالیت و لوزی نشان دهنده نتیجه‌ است. در (تصویر 3) نمونه ای از یک درخت تصمیم نشان داده شده است:

در (تصویر4) نمونه ای از یک درخت تصمیم برای یک مجموعه داده آموزش نشان داده شده است:

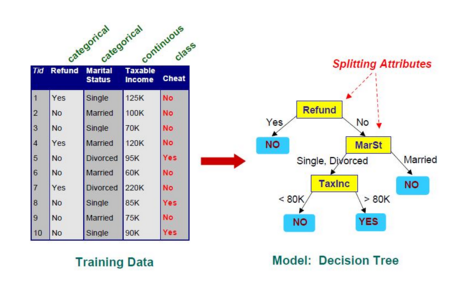
مشکل استفاده از درخت‌های تصمیم آن است که به صورت نمایی با بزرگ شدن مسئله بزرگ می‌شوند. همچنین اکثر درخت‌های تصمیم تنها از یک ویژگی برای شاخه زدن در گره‌ها استفاده می‌کنند در صورتی که ممکن است ویژگی ها دارای توزیع توأم باشند. ساخت درخت تصمیم در برنامه‌های داده کاوی حافظه زیادی را مصرف می‌کند زیرا برای هر گره باید معیار کارایی برای ویژگی‌های مختلف را ذخیره کند تا بتواند بهترین ویژگی را انتخاب کند [8]. با این حال می توان با استفاده از الگوریتم هایی درخت تصمیم بهینه ای در بازه ی زمانی قابل قبولی تشکیل داد.از انواع این الگوریتم ها می توان به الگوریتم هانت¹⁰ ID3,C4.5, CART, SPRINT اشاره کرد که در ادامه به معرفی الگوریتم هانت می پردازیم.

لگوریتم هانت :

دراین الگوریتم یک درخت تصمیم گیری با یک روند بازگشتی با جداسازی داده های آموزش به زیر مجموعه هایی که به طور پی در پی خالص تر می شوند، توسعه می یابد.
فرض کنید که { D }_{ t } مجموعه داده های آموزشی باشد که می خواهیم در رابطه با قرار گرفتن یک مقدار از آن در گره t ام تصمیم گیری کنیم.

• اگر { D }_{ t } شامل رکوردهایی باشد که متعلق به کلاس یکسان { y }_{ t ) هستتند، آنگاه t یک گره برگ است که با { y }_{ t } برچسب گذاری می شود.

• اگر { D }_{ t } یک مجموعه ی خالی باشد، آنگاه t یک گره برگ با یک مقدار پیش فرض برای کلاس { y }_{ d } برچسب گذاری می شود.

• اگر { D }_{ t } شامل رکوردهایی باشد که متعلق به بیش از یک کلاسند، یک صفت را برای جداسازی داده ها به زیرمجموعه هایی کوچکتر تست می کنیم. و برای هر زیر مجموعه رویه را به صورت بازگستی به کار می گیریم[9].

۲.۳.۲. ماشین بردار پشتیبانی ( Support Vector Machine; SVM )

هدف این دسته الگوریتم ها تشخیص و متمایز کردن الگوهای پیچیده در داده ها (از طریق کالسترینگ، دسته بندی، رنکینگ، پاکسازی و غیره)می باشد. مبنای کاری دسته بندی SVM دسته بندی خطی داده ها است و در تقسیم خطی داده ها سعی می شود خطی را انتخاب کنیم که حاشیه اطمینان بیشتری داشته باشد.اگر داده های آموزشی جدایی پذیر خطی باشند، می توان دو ابر صفحه در حاشیه نقاط در نظر گرفت؛ به طوری که هیچ نقطه مشترکی نداشته باشند. سپس می بایست فاصله آنها را به حداکثر رساند. نزدیکترین داده های آموزشی به ابر صفحه های جدا کننده بردارپشتیبان نامیده می شوند.

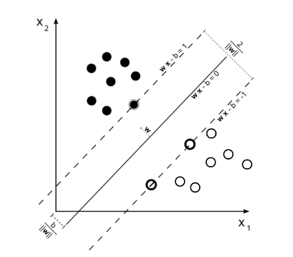
در (تصویر 6) ، دو دسته از داده های آموزش به وسیله ی یک ابر صفحه دسته بندی شده اند.

در مسایلی که داده ها بصورت خطی جداپذیر نباشند داده ها به فضای با ابعاد بیشتر نگاشت پیدا میکنند تا بتوان آنها را در این فضای جدید بصورت خطی جدا نمود[10] .

۳. آزمایش‌ها

در این بخش به پیاده سازی برخی از روش های اشاره شده در بخش های قبلی پرداخته شده است.نحوه ی پیاده سازی از طریق این لینک در گیت هاب قابل مشاهده است.

۳.۱. داده ها :

همان طور که در بخش اول اشاره شد ،داده های خام، تصاویر سطح سنگ ها می باشد که در قسمت پیوند های مفید به عنوان مجموعه داده آموزشی قرار داده شده است.تعداد تصاویر 148 تا می باشد که هرکدام حدود 60 کیلو بایت می باشد. این تصاویر متعلق به چهار نوع سنگ به نام های a,b,c,d می باشند.بنابراین برای هر نوع سنگ 37 تصویر در نظر گرفته شده است.این تصاویر رنگی می باشند.برای آزمایش از هر نوع سنگ 10 تصویر جهت آموزش و 27 تصویر دیگر به عنوان داده ی جدید جهت آزمودن دقت روش به کار رفته ، مورد استفاده قرار گرفته شده است.

۳.۲. پیش پردازش:

برای پیاده سازی روش ماتریش تکرار جهت استخراج ویژگی های بافت به وسیله ی ماتریس تکرار لازم است سطوح تیرگی تصاویر (یا به اصطلاح حالت سیاه سفید تصاویر) را به دست آوریم.

۳.۳. استخراج ویژگی ها :

در این مرحله با به دست آوردن ماتریس تکرار سطوح تیرگی ، ویژگی هایی همچون عدم تجانس ¹¹ ،همبستگی ¹² و گشتاور زاویه ای مرتبه دوم¹³ قابل استخراج هستند.

۳.۴. دسته بندی:

پس از استخراج ویژگی های ذکر شده ، می توان ابزار طبقه بندی ¹⁴ مورد نظر خود را تربیت نمود . در این آزمایش از درخت تصمیم و ماشین بردار پشتیبانی که در بخش 2 به شرح آنها پرداخته شد ،استفاده شده است.
در این آزمایش ، با در نظر گرفتن هر یک از ویژگی های عدم تجانس،همبستگی و گشتاور جهت تربیت ابزار دسته بندی به طور جداگانه ، داده های جدید دسته بندی می شوند و دقت هرکدام برای دسته بندی مورد بررسی قرار می گیرند. سپس نتیجه را برای ترکیب هر سه ویژگی بررسی می کنیم.دقت ها با فرمول زیر محاسبه شده اند، به طوری که incorrect تعداد نمونه هایی است که در دسته ی نادرست قرار داده شده اند.totaltest تعداد کل نمونه های آزمون است.

۳.۴.۱. عدم تجانس:

در این مرحله ابزار دسته بندی فقط با میزان عدم تجانس مورد تربیت قرار می گیرد.بنابراین با روش دسته بندی درخت تصمیم و svm به ترتیب به دقت 81.48% و 73.14%دست یافتیم .

۳.۴.۲. همبستگی:

به طور مشابه،در این مرحله ابزار دسته بندی فقط با میزان همبستگی مورد تربیت قرار می گیرد.بنابراین با روش دسته بندی درخت تصمیم و svm به ترتیب به دقت 48.14% و 45.37%دست یافتیم .

۳.۴.۳. گشتاور زاویه ای مرتبه دوم:

در این مرحله نیز ابزار دسته بندی فقط با میزان گشتاور زاویه ای مرتبه دوم مورد تربیت قرار می گیرد.بنابراین با روش دسته بندی درخت تصمیم و svm به ترتیب به دقت 66.66% و 53.70%دست یافتیم .

۳.۴.۴. ترکیب هر سه ویژگی:

در این مرحله ابزار دسته بندی با هر سه ویژگی مورد تربیت قرار می گیرد.بنابراین با روش دسته بندی درخت تصمیم و svm به ترتیب به دقت 84.25% و 82.40%دست یافتیم .

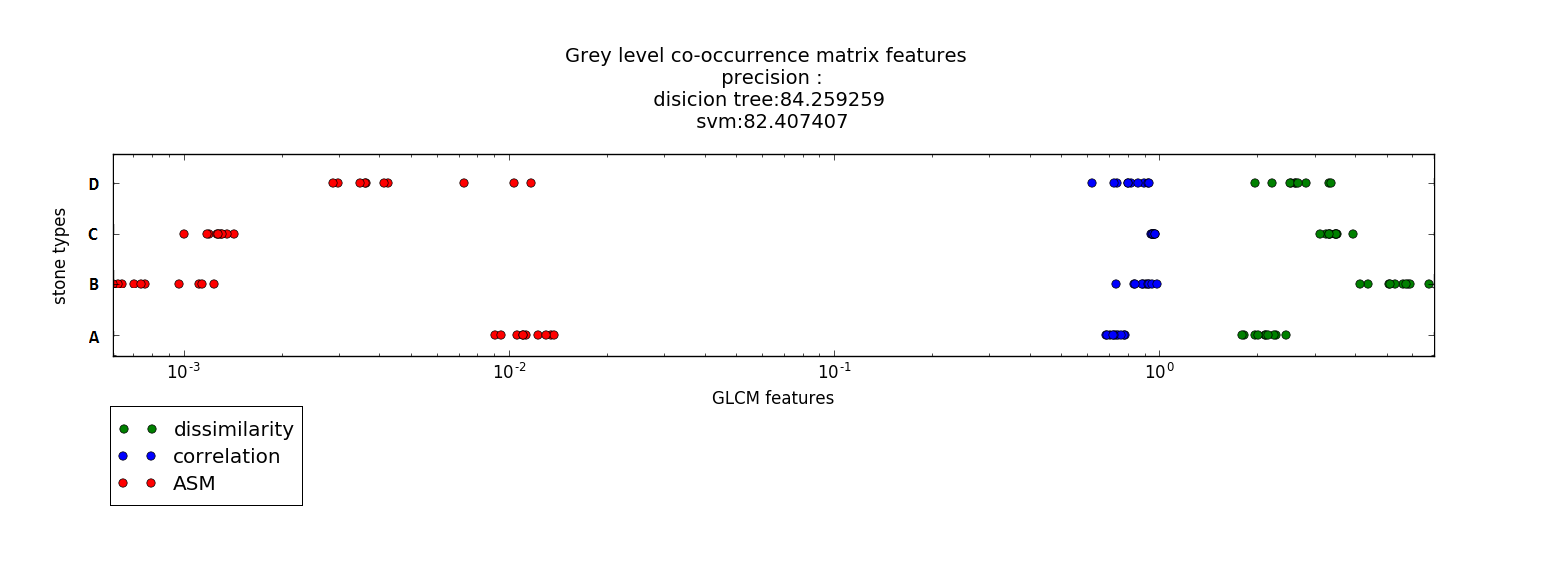
در (تصویر 7) نمودار ویژگی های ماتریس تکرار سطوح تیرگی برای داده های آموزشی مربوط به هر چهار نوع سنگ می باشد.همان طور که مشاهده می کنید ،میزان ویژگی های داده های آموزشی مربوط به هر نوع از سنگ ها تقریبا در یک محدوده قرار دارند و متراکم می باشند.
ویژگی گشتاور زاویه ای مرتبه دوم برای گونه های a و d مشابه است و در یک محدوده قرار میگیرند(به نقاط قرمز رنگ برای a و d توجه شود).این ویژگی برای گونه های c و b نیز مشابه است اما با گونه های a و d متفاوت است.بنابراین می توان از گشتاور زاویه ای مرتبه دوم برای جدا نمودن گوه های a,d از b,c استفاده نمود.ویژگی همبستگی برای تشخیص گونه ی a از سایر گونه ها مناسب است (به نقاط آبی رنک برای a و ارتباط آن با سایر نقاط آبی برای گونه های دیگر توجه شود.)ویژگی عدم تجانس به دلیل اینکه برای هر گونه محدوده ی مشخصی دارد و این محدوده با محدوده ی سایر گونه ها هم پوشانی کمی دارد ، برای تفکیک گونه ها می تواند مناسب باشد(به محدوده ی نقاط سبز رنگ برای هر گونه توجه شود.)
این تحلیل ها که از بررسی نمودار فوق به راحتی قابل دستیابی هستند، دقت های به دست آمده در مراحل ذکر شده را توجیح میکنند.برای نمونه همانطور که از نمودار برداشت شد، ویژگی عدم تجانس برای تفکیک هر چهار نوع سنگ ،مناسب است.دقت دسته بندی با این ویژگی نیز همان گونه که در بخش قبل اشاره شد،نسبت به سایر ویژگی ها مناسب تر است.
اما با توجه به نتایج آزمایش ها ترکیب هر سه ویژگی جهت تربیت ابزار دسته بندی و تفکیک گونه ها از یکدیگر ،روشی دقیق تر می باشد.

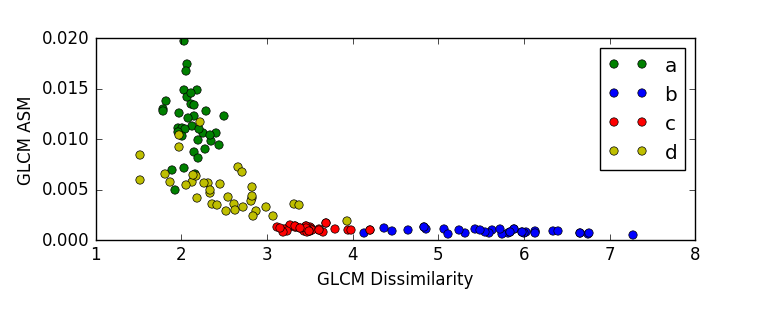
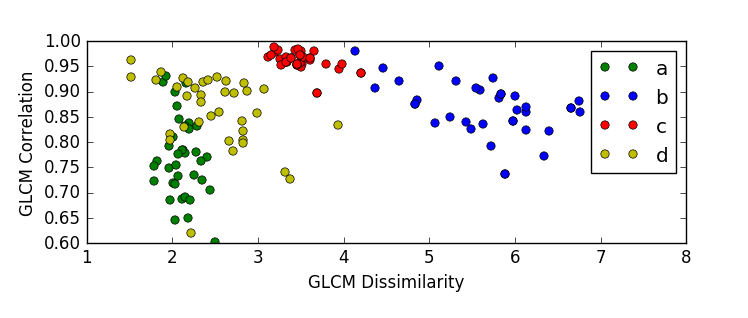
در دو تصویر فوق پراکندگی 148 سنگ موجود در مجموعه داده ها بر اساس سه ویژگی عدم تجانس ، گشتاور زاویه ای مرتبه دوم و همبستگی قابل مشاهده است،
بر اساس نمودار سه نمونه از گونه ی d در محدوده ی عدم تجانس گونه ی c قرار گرفته است.همچنین یک نمونه از گونه ی c در محدوده ی عدم تجانس گونه ی b قرار گرفته است.به طور مشابه نمونه های دیگری از قرار گرفتن سنگ ها در محدوده ی ویژگی های مربوط به یک گونه ی نادرست در این دو نمودار قابل مشاهده است، این همپوشانی ها موجب بروز خطا در امر دسته بندی می گرددند.لذا در مراحل آینده سعی می شود این هم پوشانی ها کاهش یافته و دقت دسته بندی را افزایش یابد.

۴. کارهای آینده

۵. مراجع

[1] ر.مسعودی، تشخیص نوع سنگ‌های تزئینی با استفاده از ویژگی‌های بافت آن‌ها، پایان‌نامه کارشناسی، دانشگاه علم و صنعت ایران، ۱۳۹۱ دریافت

[2] Petrou, M. & Sevilla, P.G. (2006). Image Processing: Dealing With Texture. West Sussex, England: John Wiley & Sons Ltd.
[3]Li X, Chen S, Shyu M and Furht B, "An Effective Content-Based Visual Image Retrieval System, " in 26th IEEE Computer Society International Computer Software and Applications Conference (COMPSAC), Oxford, 2002, pp. 914- 919.
[4]Nahid Khazenie,University Corporation for Atmospheric Research and Boulder, CO 80301, Kim Richardson,Naval Research Laboratory, Monterey, CA 93943-5006,"Comparison of Texture Analysis Techniques in Both Frequency and Spatial Domains for Cloud Feature Extraction".
[5]https://en.wikipedia.org/wiki/Voronoi_diagram
[6]Yoshinori Dobashi, Toshiyuki Haga, Henry Johan, Tomoyuki Nishita,"A Method for Creating Mosaic Images Using Voronoi Diagrams" .
[7]A. Materka, M. Strzelecki, "Texture Analysis Methods – A Review", Technical University of Lodz, Institute of Electronics, COST B11 report, Brussels 1998
[8]Y. Yuan and M.J. Shaw, "Induction of fuzzy decision trees".Fuzzy Sets and Systems 69 (1995), pp. 125–139
[9] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, "Introduction to Data Mining" ,Pearson Education,2006.
[10]Christopher J. C. Burges. "A Tutorial on Support Vector Machines for Pattern Recognition". Data Mining and Knowledge Discovery 2:121 - 167, 1998
[11]JAMES ENNS,"Seeing textons in context",Dalhousie University, Halifax, Nova Scotia, Canada
[12]B. Julesz. "Visual Pattern Discrimination". _IRE Transactions on Information Theory, 8:84-92, 1962.
[13]B. Julesz, E. N. Gilbert, L. A. Shepp, and H. L. Frisch. Inability of Humans to Discriminate between Visual Textures that Agree in Second-order Statistics- revisited". Perception, 2:391-405, 1973
[14]B. Julesz. "Textons, the Elements of Texture Perception, and their Interactions. "Nature, 290:91-97, March 1981.
[15]Haralick, R.M., Shanmugam, L., Dinstein, “Textural features for image classification”, IEEE Trans. Systems, Manufact, Cybernet., Vol. 3, Issue 6, pp. 610-621, 1973.
[16]M. Partio, B. Cramariuc, M. Gabbouj, and A. Visa, “Rock texture retrieval using gray level co-occurrence matrix” Norsig2002, Oct 2002

پیوندهای مفید

• مجموعه داده آموزشی

• کتابخانه یادگیری ماشین در پایتون